PROPORÇÃO ÁUREA

A PROPORÇÃO ÁUREA. 

 

Tudo no Universo Segue Esta Proporção 

''Lucas Robert''

proporção Áurea ou Números de Ouro foi elaborado pelo matemático e escultor grego Phideas (Fídias) em a.C. 455, sendo que, a teria utilizado para construir o Parthenon. No século 13, o italiano Leonardo Fibonacci no ano de 1.210 utilizou a tabela da proporção áurea em tudo que fazia… A Proporção Áurea é muito mais abrangente, e muito mais fascinante do que você possa imaginar. 

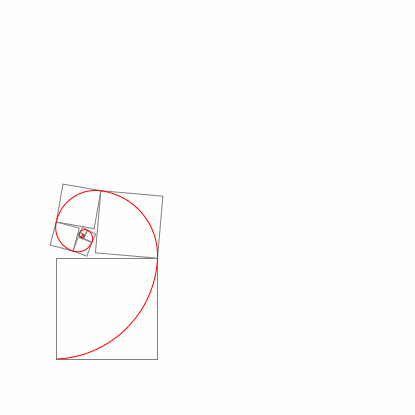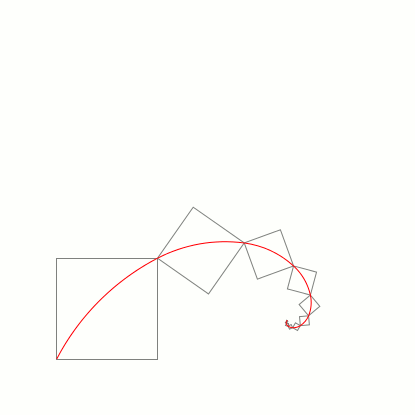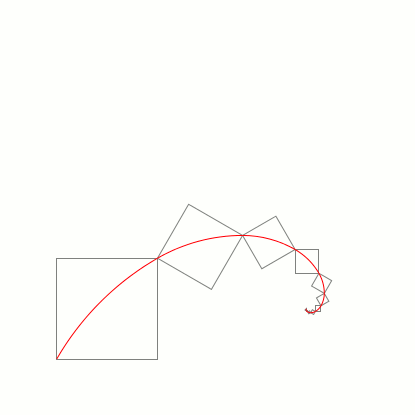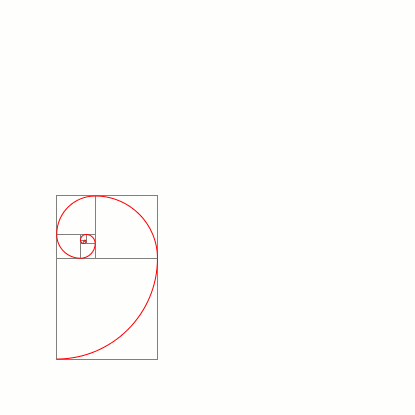
 Para simplificar, Números de Ouro ou Proporção Áurea é uma constante algébrica irracional obtida quando temos um retângulo e dividimos o valor do seu lado maior pelo valor do seu lado menor, e o resultado é obtido pela razão igual a 1,6180339887… ou, arredondando, 1,6180. A imagem a seguir vai lhe ajudar a entender o valor da razão de 1,6180: 

 

Quem inicialmente elaborou a Proporção Áurea / Números de Ouro? 

Os Números de Ouro / Proporção Áurea tem a ver com o escultor e matemático grego Phidias, que acredita-se, provavelmente ele aplicou o conceito quando projetou o Parthenon, isso lá no século 5 a.C. Em sua parte frontal, o comprimento e a altura formam uma perfeita Proporção Áurea. Tudo no Parthenon tem a razão de 1,6180… 

 

Curiosamente, tudo que tem esta razão, teoricamente, você irá gostar e vai usar, uma vez que a razão de 1,6180 nos agradam no “Visualizar, no “Utilizar”, no “Pegar”, Etc… Seguem quatro bons exemplos: 

Nos agradam em “Visualizar” – Tela do Celular J7: 

 

Outro grande exemplo que nos agradam em “Visualizar” – Campo de Futebol: 

 

Nos agradam em “Utilizar” – TV 42″: 

 

Nos agradam em “Pegar” – Cartão de Crédito: 

 

MORAL DA HISTÓRIA 

Números de Ouro / Proporção Áurea é a fórmula matemática que lhe agradará tudo que tiver a razão de 1,6180 (A / B = 1,6180). 

 

REFLEXÃO DA HISTÓRIA 

O grego Phidias não foi o único que se tornou fã da Proporção Áurea! No começo do século 13, o italiano Leonardo Fibonacci descobriu as propriedades únicas em uma sequência de Números de Ouro: 

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584…]